Since de beginning of this year I’m discovering NMT, with the practice of OpenNMT. Quickly, I was puzzled by the strange behaviour of the training. The scenario is this one:
- in the first 2 ou 3 epochs, I get a very interesting model, already doing quite good draft translations. It lets me hope for a wonderful evolution in next epochs… but,
- for several epochs, the model is very slowly improving. It lets me think it will take a lot of time to handle sentences in detail, and produce good translations… but,
- then, the quality of the translations is surprisingly decreasing. While the training PPL is still decreasing, both the validation PPL and the translation quality seem to go in a sad way…
NMT literature speaks of over-fitting, and NMT tools are using the early stopping procedure to avoid it. Well…
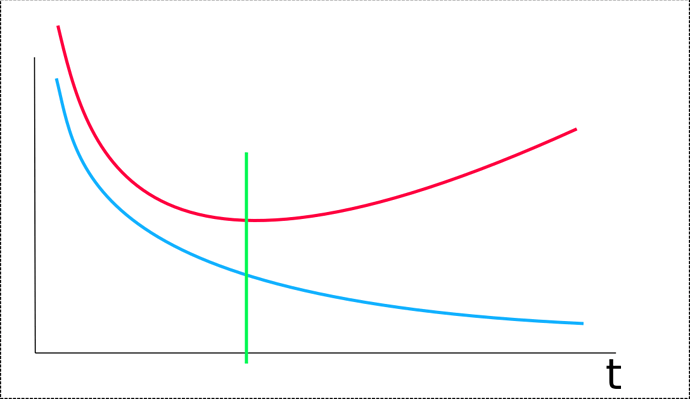
But, in my mind, in a good learning system, the learning curve should not be like this:
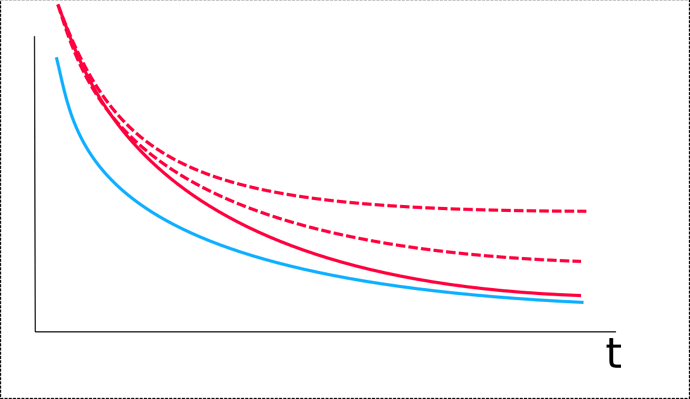
It should rather be like this:
Over-fitting as something to do with the bias-variance tradeoff, thus with the number of freedom degrees of the learning system, thus with the size of the network. In the above curve, it should not be “t” in abscisse, but “N”, the number of parameters to tune, and each point should be the training and validation error obtained at the full convergence of the system. But, with NMT behaviour explained above, there isn’t any possibility to have a good full convergence.
Of course, the obtained model on large epochs looks like doing over-fitting, but, for me, it’s rather the result of an instability of the training. It’s very strange that the system is learning something and then, damage this learning. An over-fitting system is doing random things outside of the training points, it should even not be able to really learn something.
I have the idea that this instability is due to the fact that the vector layers are changing the input/output data topology while the main network is trying to find its convergence. Training data and the main network model, to make the learning PPL decreasing, are over-fitting / over-matching together in a non ‘pertinent’ way.
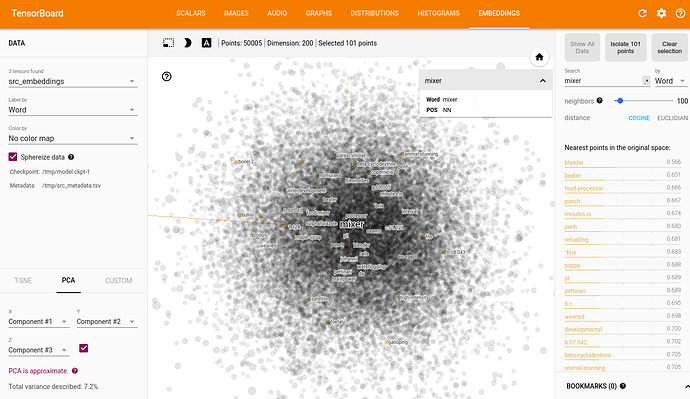
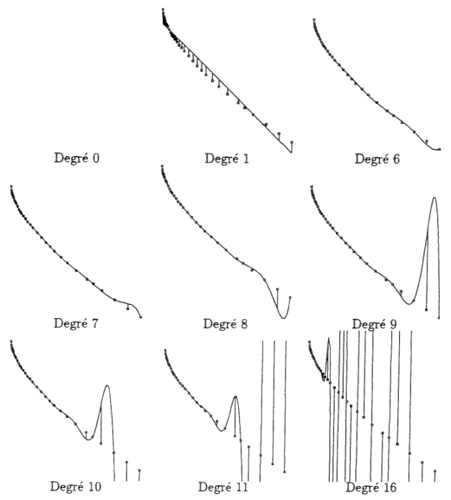
In fact, the data distribution built by ONMT is quite complex, and it’s hard for a human to find something pertinent in it:
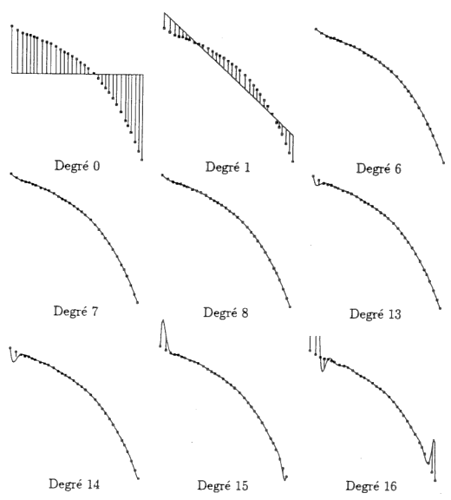
I did my test starting with the w2v distribution:
I started with a learning rate of 1.5, decreasing of 0.95 at each epoch. In this first run, ONMT was training with FIXED embeddings. I got this learning curve, learning rate was 0.7315 at epoch 15:
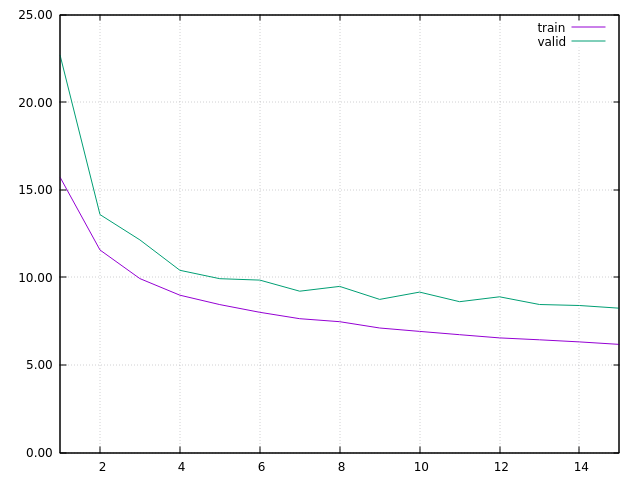
PS (Mar 13, 2017) : there was a bug somewhere in the second part of the test below. The embeddings are in fact not changing. Thus, this experimentation shows that the training is stable, with no over-fitting effect, with a fixed pre-trained w2v embeddings. It doesn’t properly show that this training is still stable when the embeddings are again updated in the training.
At this step, I considered I got a main net model properly built for matching the w2v data distribution, and I restarted the training at epoch 16, with embeddings TRAINING. In order to stress a bit the system, and test its stability, I started with a learning rate at 1.0, decreasing by 0.95 at each epoch. I then got this learning curve:
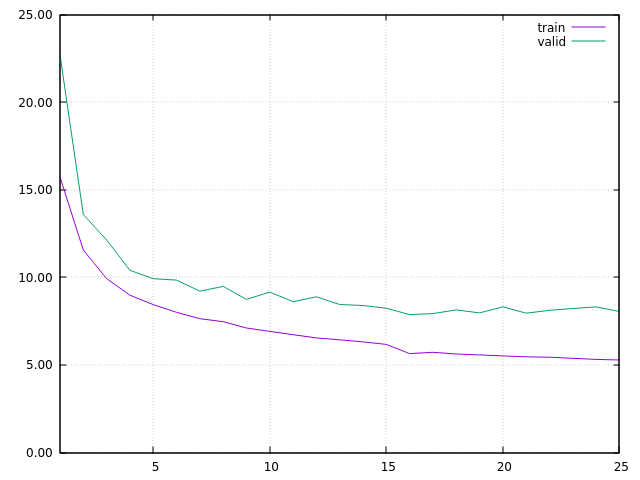
The main interesting thing is that, in spite of the increasing validation PPL, the translation is really improving. I think the increasing validation PPL is due to several facts:
- I’m using real industrial data. For many reasons, both the training and the validation sets are full of errors. So, while the translation quality of ONMT model is increasing, good translations are not matching some wrong validation data.
- there are several way to built good translations. Even when ONMT translation are good, they are not always matching the human translations in the validation set. Often, in fact, the human translation is even not totally accurate to the original full content.
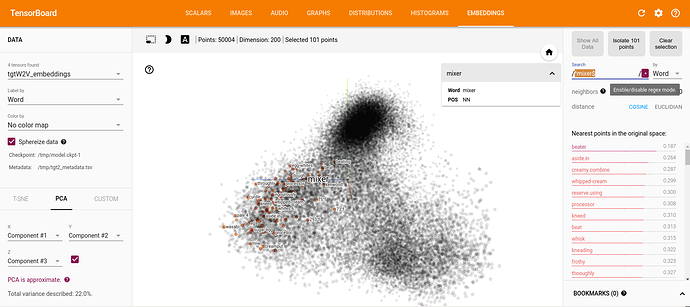
To obtain this, ONMT have made very tiny changes on the w2v data distribution. It’s much more visible while looking at the cos-dist values (on the right panel) than looking at the distribution itself (on the middle):
The training is still running. Now, it looks stable, and always seems to improve.